Если вы живете на Севере, то вы уже столкнулись с этим — система домов Плацидуса не строится за полярным кругом.
В этой статье вы найдете таблицу, которая расширяет систему домов до самого крайнего Севера. Скорее всего вам придется построить гороскоп вручную, так как не все программы смогут его рассчитать.
Но, согласитесь, это лучше, чем жить без понимания как же выглядит ваш гороскоп рождения.
[toc]
Система домов Плацидуса
Представьте небесную сферу:
- Тысячи светящихся точек восходят на восточном горизонте,
- Затем они доходят до зенита,
- Начинают снижаться, и…
- Окончательно заходят на западном горизонте.
Мысленно проследите за движением любой выбранной точки.
- Путь от восхода до кульминации называют дугой восхождения.
- Путь от кульминации до захода называют дугой заката.
Теперь мысленно отмерьте 1/3 каждой дуги восхождения. Концы этих отрезков образуют разделительную линию 12 дома гороскопа - самого таинственного сектора карты.

Если планета окажется между горизонтом и границей 12 дома, то она будет находится внутри 12 дома в системе Плацидуса.
Аналогично, если отложить путь в 2/3 для восходящих дуг, мы получим границу 11 дома.
И так далее по аналогии. Таким образом составляется система домов Плацидуса. Если планета попадает в одиссеи н из домов, то ее влияние на жизнь человека сильно меняется.
Вы можете узнать подробнее о том, за что отвечают определенные дома в астрологии.
На рисунке ниже я изобразил как вершина 12 дома пересекает зодиакальный круг недалеко от асцендента.
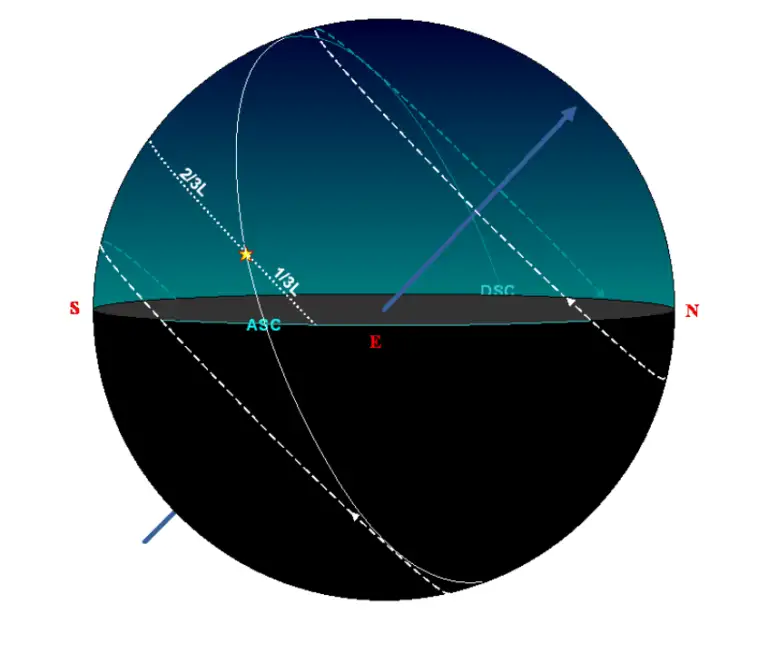
Теперь посмотрим на ту же картинку глазами жителя крайнего Севера.
Система домов Плацидуса за полярным кругом
Чтобы понять причину исчезновения куспидов в системе домов Плацидуса за полярным кругом достаточно взглянуть на рисунок ниже:
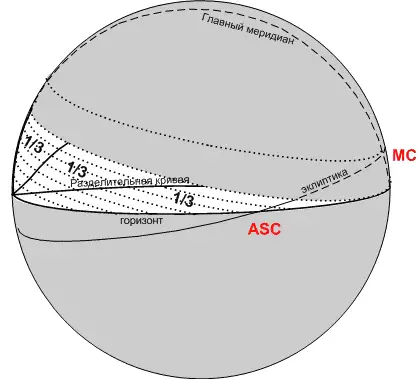
Зодиакальный круг — это плоскость эклиптики, внутри которой находятся планеты в знаках. Как видно, на крайнем Севере часть знаков не восходит и не заходит.
Они как бы постоянно крутятся над горизонтом. Следовательно, для них нет точки восхода, нам не от чего откладывать треть пути восходящей дуги…
Это как раз та серая область, где находится слово «эклиптика» на рисунке.
(Примечание. Любой хороший астролог разбирается как в небесной геометрии, так и в составлении прогнозов. Узнайте, есть ли у вас талант к изучению звездной науки, пройдя простой астрологический тест).
[promoTest]
Однако у нас есть максимально высокая точка зодиака — это вершина неба, MC.
Но я предлагаю сразу разделить понятия — математическую точку середины неба и куспид десятого дома в системе домов Плацидуса.
Математическая точка середины неба
Это точка пересечения эклиптики и небесного меридиана над горизонтам в данный момент времени.
Эта точка существует на всех широтах, включая северный полюс, хотя в заполярных широтах она два раза в сутки меняет свою позицию (эффект полярной переориентации).
Ее расчету было посвящено предыдущее исследование, где и была составлена таблица ее положений.
Вершина 10 дома гороскопа в системе домов Плацидуса
Это некогда взошедшая точка зодиакального круга, которая прошла 100% восходящей дуги.
До полярного круга эти точки неразличимы. Но за полярным кругам они уже не равны.
Однако приведенные выше примеры не означают, что система домов Плацидуса не применима в Заполярье. Рассмотрим еще один рисунок:
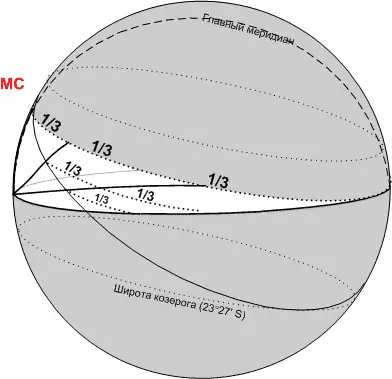
Здесь показан момент формирования куспидов 12-го и 11-го домов в системе Плацидуса. Наличие подобных моментов говорит лишь о том, что не все куспиды в системе домов Плацидуса исчезают за полярным кругом.
Часть из них, действительно, нельзя вычислить – наличие таких «пустот» является интереснейшим предметом исследований и особых интерпретаций астрологов.
Но часть домов остается весьма определяемой. Следовательно, к ним можно применять, хотя и с особой осторожностью, уже известный астрологический аппарат.
Я верю, что наличие расширенной до заполярных широт таблицы системы домов Плацидуса может помочь астрологам исследовать вопрос планетарного воздействия в крайних северных широтах.
Далее в этой статье я опишу математическую модель построения системы домов Плацидуса.
Вы можете смело пролистать эту главу и сразу перейти к результатам расчетов - таблице домов Плацидуса за полярным кругом.
Математические основы системы домов Плацидуса
Формулы, описывающие связь между различными системами отсчета выведены в предыдущей работе, посвященной расчету угловых домов за полярным кругом. Поэтому здесь я приведу их без вывода.
В качестве основной схемы расчетов примем следующую последовательность:
- Перейдем в систему отсчета, связанную с неподвижными звездами (экваториальная система координат)
- Найдем множество точек дуги восточного горизонта наблюдателя в виде декартовых координат (xeq(h),yeq(h),h) в экваториальной системе координат в 0:00 звездного времени. Здесь и далее h выступает как свободный параметр в параметрическом уравнении дуги
- Придадим динамику вращения найденным точкам, используя матрицы вращения.
- Найдем множество точек дуги главного небесного меридиана над головой наблюдателя в виде (xeq(h),yeq(h),h) в экваториальной системе координат в 0:00 звездного времени
- Аналогично, придадим динамику найденным точкам, используя матрицы вращения
- Найдем множество длин дуг дневных восхождений в виде l(h) в произвольный момент времени
- Вычислим треть длины найденных дуг. Найдем множество точек разделительной кривой в виде (xeq(h),yeq(h),h) в экваториальной системе координат в произвольный момент времени.
- Теперь найдем множество точек эклиптики в виде (xeq(h),yeq(h),h) в экваториальной системе координат
- Далее найдем точки пересечения разделительной кривой и окружности эклиптики в данный момент времени – решим систему уравнений двух параметрических кривых относительно свободного параметра h.
- Переведем найденные точки эклиптики в градусы зодиакального круга.
Кривая горизонта с восточной стороны
Система уравнений ниже описывает связь между
- локальными декартовыми координатами наблюдателя и
- экваториальными декартовыми координатами системы неподвижных звезд:
Где $\beta=90$°-широта наблюдения, $\phi=LST/24*360°-90°$, $LST$-локальное звездное время.
Давайте в 0:00 звездного времени направим декартовы оси экваториальной системы как указано на рисунке ниже. А именно, ось $Z_{eq}$ направим на северный полюс мира, а $X_{eq}$ на точку Востока:
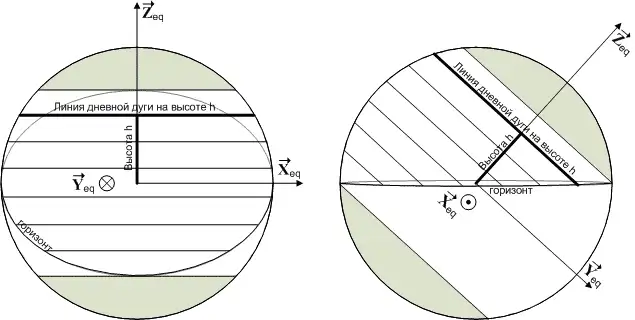
Далее рассмотрим восточную окружность горизонта в экваториальной системе координат в 0:00 звездных суток.
Окружность описывается следующим набором уравнений
$$\begin{cases} z = 0 \\ x^2 + y^2 = 1 \\ y_{eq} > 0 \end{cases}$$
Это дает, в итоге, параметрическое уравнение дуги:
$$\begin{cases} x_{eq} &= \sqrt{1 - h^2} \\ y_{eq} &= h\frac{\cos\beta}{\sin\beta} \\ z_{eq} &= h\\ h &\in [-\sin\beta, \sin\beta] \end{cases} $$
В произвольный момент звездного времени $LST$ параметрическое уравнение дуги будет выглядеть следующим образом:
где $\Delta\phi=ST/24*360°$.
Верхняя дуга главного меридиана
Найдем теперь дугу меридиана над горизонтом в 0:00 звездных суток. Уравнение дуги выглядит как обычно:
$$\begin{cases} y = 0 \\ x^2 + z^2 = 1 \\ z \ge 0 \end{cases}$$
и дает параметрическое уравнение множества ее точек
$$\begin{cases} x_{eq} = \sqrt{1-h^2}\sin\Delta\phi \\ y_{eq} = -\sqrt{1-h^2}\cos\Delta\phi \\ z_{eq} = h\\ h \in [-\sin\beta, \sin\beta] \end{cases} $$
где $\Delta\phi$ в произвольный момент звездного времени $\Delta\phi=ST/24*360°$.
Разделительные кривые
Итак, для каждого из значений $h \in [-\sin\beta, \sin\beta]$ мы нашли множество точек
- $(x_1, y_1, h)$ дуг восточного горизонта и
- $(x_2, y_2, h)$ верхней части главного меридиана
в экваториальной небесной системе координат.
Найдем теперь длины дуг восхождений точек небесной сферы. Для этого рассмотрим окружность, которой принадлежит дуга восхождения (она обозначена пунктиром на рисунке).

На пунктирной окружности координатам $(x_1, y_1)$ и $(x_2, y_2)$ соответствуют два угла $\phi_1$ и $\phi_2$ соответственно. Они определяются из системы уравнений:
$$\begin{cases} x_{1,2} = \cos\phi_{1,2} \\ y_{1,2} = \sin\phi_{1,2} \end{cases}$$
Разница $\phi_1 - \phi_2$ как раз равна угловой величине дуги восхождения. Одна треть дуги восхождения характеризуется углом $\phi_3$, синус и косинус которого равны координатам $(x, y)$ трети длины дуги на плоскости дневной окружности.
Таким образом, параметрическое уравнение разделительной линии будет описываться следующей системой:
$$\begin{cases} x_{eq} = \cos\left(\phi_1(h) - \frac{\phi_1(h) - \phi_2(h)}{3}\right) \\ y_{eq} = \sin\left(\phi_1(h) - \frac{\phi_1(h) - \phi_2(h)}{3}\right) \\ z_{eq} = h\\ h \in [-\sin\beta, \sin\beta] \end{cases}$$
В самом общем случае параметрическое уравнение разделительных окружностей можно записать в виде:
$$\begin{cases} x_{eq} = \cos\left(\phi_1(h) - \frac{\phi_1(h) - \phi_2(h)}{3}\right) \\ y_{eq} = \sin\left(\phi_1(h) - \frac{\phi_1(h) - \phi_2(h)}{3}\right) \\ z_{eq} = h\\ h \in [-\sin\beta, \sin\beta] \end{cases}\tag{1}$$
При этом:
- N=0 определяет куспид 1-го дома;
- 1 определяет куспид 12-го дома;
- 2 определяет куспид 11-го дома;
- 3 определяет куспид 10-го дома;
- 4 определяет куспид 9-го дома;
- 5 определяет куспид 8-го дома.
Окружность эклиптики
Связь между эклиптическими и экваториальными координатами описывается следующей системой уравнений:
$$\begin{cases} x_{ecl} = x_{eq}\cos\alpha + z_{eq}\sin\alpha \\ y_{ecl} = y_{eq} \\ x_{ecl} = -x_{eq}\sin\alpha + z_{eq}\cos\alpha \end{cases}$$
Уравнение линии эклиптической окружности определяется условиями
$$\begin{cases} x_{ecl}^2 + y_{ecl}^2 = 1 \\ z_{eql} = 0 \end{cases}$$
что, в итоге, и дает параметрическое уравнение точек зодиакального круга на небесной сфере в экваториальной системе координат:
$$\begin{cases} x_{eq} = h\frac{\cos\alpha}{\sin\alpha} \\ y_{eq} = \pm \sqrt{1 -\frac{h^2}{\sin\alpha^2}} \\ z_{eq} = h\\ h in [-\sin\alpha, \sin\alpha] \end{cases}\tag{2}$$
Куспиды домов
- Уравнение (1) определяет множество точек $(x_1,y_1,h)$ разделительной кривой в данный момент времени,
- В то же время уравнение (2) определят множество постоянных точек $(x_2,y_2,h)$ зодиакального круга, жестко связанных с небесной сферой и не зависящих от времени.
Задача поиска куспидов домов теперь сводится к поиску пересечения двух кривых – дуги зодиакального круга и разделительной кривой на интервале
$h \in [-\min(\sin\alpha\sin\beta), \max(\sin\alpha\sin\beta)]$
Для решения этой задачи можно использовать различные численные методы.
Я прибегну к следующему: две параметрические кривые пересекаются при некотором значении параметра $h$, если радиус вектор между двумя точками этих кривых при данном $h$ равен нулю. То есть
$$ \sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2} = 0 $$
Таким образом, задача свелась к поиску нулей (их будет минимум 2 в заполярных широтах) функции
Если на указанном отрезке существует решение, следовательно существует и куспид соответствующего дома.
После нахождения корня уравнения $R(h)=0$, нам в итоге станут известны экваториальные координаты точки пересечения эклиптики и разделяющей кривой.
Переводя указанные экваториальные координаты в эклиптическую систему по приведенным выше уравнениям, мы сразу получаем координаты куспида $(x_{ecl},y_{ecl},0)$ на плоскости эклиптики.
Используя далее соотношения
$$\begin{cases} x_{ecl} = \cos(\phi_{cusp} + 90°) \\ y_{ecl} = \sin(\phi_{cusp} + 90°) \end{cases}$$
мы, наконец, находим угол куспида дома на зодиакальном круге. Полный математический расчет вы можете скачать по этой ссылке:
Итак, таблица
Если вы достаточно быстро пролистали математически основы системы домов Плацидуса в Заполярье, то сейчас самое время снова вчитаться в текст.
Так как ниже я привожу ссылку на результаты своих расчетов. Итак, представляю вам расширенную таблицу….
Система домов Плацидуса (только таблица)
Скачивайте ее себе и пользуйтесь на здоровье.
Расчет домов - это лишь малая часть прогностической астрологии. Узнайте, насколько вы талантливый астролог и как быстро звезды могут покориться вам!
[promoTest]

